Lernaufgabe 6: Einflüsse auf Auswahlkriterien von Leitungen ermitteln
Hier findest du die Aufgaben ohne Lösungen.
Leitungen und Kabel haben die Aufgabe Elektroenergie zu übertragen. Sie müssen entsprechend der Einsatzbedingungen ausgewählt werden.
Leitungen werden nach dem Bemessungsstrom, der Bemessungsspannung, der Strombelastbarkeit und dem zulässigen Spannungsfall ausgewählt.
Aufgabe 1
Nenne Einflüsse, die den Betriebsstrom von Leitungen hauptsächlich bestimmen.
- Quellenspannung
- Verbraucherwiderstand
Aufgabe 2
Berechne den zu erwartenden Betriebsstrom einer elektrischen Heizung (\(230\ V / 2,8\ kW\)), wenn diese mit Vollast an \(230\ V\) betrieben wird.
\(P=U\cdot I\)
\(\Leftrightarrow I=\frac{P}{U}=\frac{2800\ W}{230\ V}=12,17\ A\)
Aufgabe 3
Ermittle den Querschnitt einer NYM-Leitung, welche den in Aufgabe 2 errechneten Strom führen kann. Als Bedingungen für die Leitung sollen gelten: Verlegeart C, zweiadrige betriebsstromführen Leitung, Umgebungstemperatur \(30\ ^\circ C\)). Nutze für die Lösung der Aufgabe die geeignete Tabelle zu Verlegearten (DIN VDE 0298).
\(I_Z=I_r=19,5\ A\)
\(A=1,5\ mm^2\)
Hinweis: Ab \(2\ kW\) eigener Stromkreis!
Aufgabe 4
Ermittle die höchstzulässigen Spannungen mit der folgende Leitungstypen betrieben werden dürfen:
| \(U_0\) in V (Leiterspannungs gegen Erde) | \(U\) in V (Leiter-Leiter-Spannung) | |
|---|---|---|
| NYM | 300 | 500 |
| NYIF | 230 | 400 |
| H03VV-F | 300 | 300 |
NYM: Mantelleitung
NYIF: Stegleitung
H03VV-F Leichte Kunststoffschlauleitung (PVC)
Aufgabe 5
Nenne Einflüsse, welche die Strombelastbarkeit von Kupferleitungen bestimmen.
- Leiterquerschnitt
- Anzahl der belasteten Adern
- Isolationsmaterial
- Verlegeart
- Häufung von Leitungen
- Umgebungstemperatur
Aufgabe 6
Recherchiere, welche Folgen eine Überlastung von Leitung hat.
- Schmelzen der Isolation
- Erzeugung hoher Stromwärme -> Brandgefahr
- Erzeugung von Kräften zwischen den Leitern bei Kurzschluss
Aufgabe 7
Ermittle anhand der Tabelle zu Verlegearten (DIN VDE 0298) die zulässige Strombelastbarkeit \(I_Z\) einer NYM-J 3x1,5 Leitung für die folgenden Verlegearten:
\(I_Z=I_r\cdot f_1\cdot f_2\)
- Verlegeart C bei \(30\ ^\circ C\) -> \(19,5\ A\)
- Verlegeart C bei \(25\ ^\circ C\) -> \(21\ A\)
- Verlegeart C bei \(40\ ^\circ C\) -> \(16,9\ A\)
- Verlegeart A2 bei \(30\ ^\circ C\) -> \(14,5\ A\)
- Verlegeart C bei \(30\ ^\circ C\) und Häufung von 4 Leitungen -> \(12,67\ A\)
Aufgabe 8
Berechne den Spannungsfall \(\Delta U\) über einer \(28\ m\) langen NYM-Leitung, die für den Anschluss der Heizung aus Aufgabe 2 verwendet wurde. Bewerte das Ergebnis, indem du es mit den i Tabellenbuch festgelegten Werten vergleichst. Hinweis: Neben \(\Delta U\) wirst du \(\Delta u\) berechnen müssen und das gegen die Festlegungen der DIN 18015 vergleichen müssen
\(R_{Leitung}=\frac{\rho\cdot l}{A}=\frac{0,0178\ \frac{\Omega\cdot mm^2}{m}\cdot 2\cdot28\ m}{1,5\ mm^2}=0,665\ \Omega=665\ m\Omega\)
\(U=R_{Leitung}\cdot I=0,665\ \Omega\cdot 12,17 A=8,09\ V\)
\(\Delta u=\frac{\Delta U\cdot 100\%}{U}=\frac{8,09\ V\cdot 100\%}{230\ V}=3,52\%\)
Nach Seite TB S. 187 gilt von Zähler zu Steckdose nach DIN 18015 ein maximal zulässiger Spannungsabfall von \(\Delta u=3\%\). Somit ist ein größerer Querschnitt zu wählen, da der Spannungsfall über der Leitung zu hoch ist.
Festigungsaufgaben
In der Hausinstallation gibt es unterschiedliche Anwendungsbereiche für den Einsatz von Leitungen.
Aufgabe A
Gib an, welche Leitungen für die Hausinstallation in Betracht kommen.
z.B.:
- isolierte Leitungen für feste Verlegung (H07V-U; NYM)
- isolierte Leitungen zum Anschluss ortsveränderlicher Verbraucher (H03VV-F; H05RR-F; H03RT-H)
Aufgabe B
Recherchiere die Bedeutung der Kennzeichnungen folgender Leitungsarten:
- H03VV-F -> harmonisiert; 300V/300V; Ader- und Mantelisolierung PVC; feindrahtig -> leichte Kunststoffschlauleitung für Haushaltsgeräte
- NYIF -> national; Kunststoffisolierung; Stegleitung; Flachleitung -> Stegleitung für feste Verlegung in trockenen Räumen
- H05RR-F -> harmonisiert; 300V/500V; Ader- und Mantelisolierung Gummi; feindrahtig-> Gummischlauchleitung für geringe mechanische Beanspruchung
- H03RT-H -> harmonisiert; 300V/300V; Aderisolierung Gummi; Mantelisolierung Textilgeflecht; feinstdrahtig -> Gummiaderleitung zum Anschluss von Elektrowärmegeräten
Aufgabe C
Gib an, welche Farbkennzeichnungen der Adern für folgende Leitungen vorgeschrieben sind.
- fest verlegt, 5-adrig, NYM-J -> braun, schwarz, grau, blau, grün-gelb
- flexibel verlegt, 3-adrig, H03VV-F -> braun, blau, grün-gelb
Aufgabe D
Gib an, welche Möglichkeiten der Verlegung von Leitungen für Installationszwecke in Frage kommen.
- im Putz
- unter Putz
- auf Putz
- im Installationsrohr oder -kanal
- in wärmegedämmten Wänden
Aufgabe E
Eine einadrige elektrische Leitung ist \(20\ m\) lang, besteht aus Kupfer und hat einen Querschnitt von \(1,5\ mm^2\). Berechne, wie groß der Widerstand der Leitung ist.
geg: \(l=20\ m\), \(A=1,5\ mm^2\), \(\rho=0,0178\ \frac{\Omega\cdot mm^2}{m}\), 1 Ader
ges: \(R\)
Lös: \(R=\frac{\rho\cdot l}{A}=\frac{0,0178\ \frac{\Omega\cdot mm^2}{m} \cdot20\ m}{1,5\ mm^2}=0,2373\ \Omega=237\ m\Omega\)
Antw: Der Widerstand der Leitung beträgt \(237\ m\Omega\).
Aufgabe F
Eine zweiadrige elektrische Leitung ist \(20\ m\) lang, besteht aus Kupfer und hat einen Querschnitt von \(1,5\ mm^2\). Berechne, wie groß der Gesamtwiderstand der Leitung ist.
geg: \(l=20\ m\), \(A=1,5\ mm^2\), \(\rho=0,0178\ \frac{\Omega\cdot mm^2}{m}\), 2 Adern
ges: \(R\)
Lös: \(R=\frac{\rho\cdot l}{A}=\frac{0,0178\ \frac{\Omega\cdot mm^2}{m} \cdot20\ m\cdot 2}{1,5\ mm^2}=0,4746\ \Omega=475\ m\Omega\)
Antw: Der Widerstand der Leitung beträgt \(475\ m\Omega\).
Aufgabe G
Der Spannungsfall über einer Leitung vom Zähler bis zum Verbraucher darf nach DIN 18015 \(3\%\) der Nennspannung (im Berliner TN-Netzsystem: \(230\ V\)) nicht überschreiten. Berechne, wie groß der absolute Spannungsfall \(\Delta U\) (in V) für dieses System ist.
geg: \(U=230\ V\), \(\Delta u=3\%\)
ges: \(\Delta U\)
Lös: \(\Delta U = U\cdot \frac{\Delta u}{100\%}=230\ V\cdot\frac{3\%}{100\%}=6,9\ V\)
Antw: Der absolute Spannungsfall beträgt \(6,9\ V\).
Aufgabe H
Der Spannungsfall über einer Leitung vom Zähler bis zum Verbraucher darf nach DIN 18015 \(3\%\) der Nennspannung (im Berliner TN-Netzsystem: \(400\ V\)) nicht überschreiten. Berechne, wie groß der absolute Spannungsfall (in V) für dieses System ist.
geg: \(U=400\ V\), \(\Delta u=3\%\)
ges: \(\Delta U\)
Lös: \(\Delta U = U\cdot \frac{\Delta u}{100\%}=400\ V\cdot\frac{3\%}{100\%}=12\ V\)
Antw: Der absolute Spannungsfall beträgt \(12\ V\).
Aufgabe I
Eine NYM-J \(3x1,5\ mm^2\)-Leitung ist \(30\ m\) lang und wird durch den Betrieb eines Heizkörpers mit \(8,7\ A\) belastet. (Leerlaufspannung \(U_0=230\ V\)). Berechne den Widerstand der Leitung und die Spannung (Spannungsfall) über der Leitung.
geg: \(l=2\cdot 30\ m\), \(U_0=230\ V\), \(I=8,7\ A\), \(\rho=0,0178\ \frac{\Omega\cdot mm^2}{m}\)
ges: \(R\), \(\Delta U\)
Lös:
\(R=\frac{\rho\cdot l}{A}=\frac{0,0178\ \frac{\Omega\cdot mm^2}{m} \cdot60\ m}{1,5\ mm^2}=0,712\ \Omega=712\ m\Omega\)
\(\Delta U=R\cdot I =0,712\ \Omega\cdot 8,7\ A=6,19\ V\)
Ant: Der Widerstand der Leitung beträgt \(712\ m\Omega\) und der Spannungsfall über die Leitung beträgt \(6,19\ V\).
Aufgabe J
An eine \(15\ m\) lange NYM-J \(3x1,5\ mm^2\)-Leitung ist eine Doppelsteckdose angeschlossen. An die eine Steckdose ist eine Mikrowelle (\(230\ V / 750\ W\)) und an die andere eine Wasserkocher (\(230\ V / 1,5\ kW\)) angeschlossen. Beide Geräte werden gleichzeitig betrieben. Die Leerlaufspannung beträgt \(230\ V\). Berechne den Belastungsstrom der Leitung und die Spannung (Spannungsfall) über der Leitung.
geg: \(U=230\ V\), \(P_{MW}=750\ W\), \(P_{WK}=1500\ W\), \(l=30\ m\), \(A=1,5\ mm^2\), \(\rho=0,0178\ \frac{\Omega\cdot mm^2}{m}\)
ges: \(I\), \(\Delta U\)
Lös:
Zuerst benötigen wir die Widerstände der beiden Verbraucher. Dafür nutzen wir als Grundformel:
\(P=\frac{U^2}{R}\Leftrightarrow R=\frac{U^2}{P}\)
\(\Rightarrow R_{MW}=\frac{(230\ V)^2}{750\ W}=70,53\ \Omega\)
\(\Rightarrow R_{WK}=\frac{(230\ V)^2}{1500\ W}=35,27\ \Omega\)
In einer Doppelsteckdose liegen die Verbraucher parallel zueinander. Somit errechnen wir den Widerstand des Gesamtverbrauchers als
\(R_V=R_{MW}||R_{WK}=\frac{R_{MW}\cdot R_{WK}}{R_{MW}+R_{WK}}=\frac{70,53\ \Omega\cdot35,26\ \Omega}{70,53\ \Omega+35,26\ \Omega}=23,51\ \Omega\)
Ferner benötigen wir den Widerstand der Leitung:
\(R_{Ltg}=\frac{\rho\cdot l}{A}=\frac{0,0178\ \frac{\Omega\cdot mm^2}{m} \cdot30\ m}{1,5\ mm^2}=0,356\ \Omega=356\ m\Omega\)
Somit ist der Gesamtwiderstand \(R_{ges}\) die Reihenschaltung aus dem Verbraucherwiderstand \(R_V\) und dem Leitungswiderstand \(R_{Ltg}\):
\(R_{ges}=R_V+R_{Ltg}=23,51\ \Omega+0,356\ \Omega=23,87\ \Omega\)
Mit dem Gesamtwiderstand \(R_{ges}\) und der Leerlaufspannung \(U_0\) können wir nun den Belastungsstrom berechnen:
\(U_0=R_{ges}\cdot I\Leftrightarrow I=\frac{U_0}{R_{ges}}=\frac{230\ V}{23,87\ \Omega}=9,64\ A\)
Schlussendlich bleibt noch der Spannungsfall über die Leitung:
\(\Delta u=R_{Ltg}\cdot I=0,356\ \Omega\cdot 9,64\ A=3,43\ V\)
Antw: Der Belastungsstrom der Leitung beträgt \(9,64\ A\) und die Spannungsfall über der Leitung \(3,43\ V\).
Aufgabe K
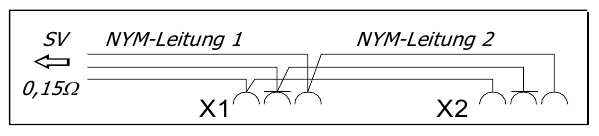
Ein Steckdosenstromkreis ist fehlerfrei installiert worden. Beide Steckdosen werden ab der Stromkreisverteilung (SV) über NYM-J \(3x1,5\ mm^2\)-Leitungen versorgt.
Schleifenwiderstandsmessungen haben an der einen Steckdose \(0,9\ \Omega\) und an der anderen Steckdose \(0,65\ \Omega\) ergeben. Bis zur Stromkreisverteilung beträgt der Innenwiderstand \(0,15\ \Omega\).
Berechne die Länge dieser beiden NYM-Leitungen.
Hinweis: Verdeutliche dir zuerst von wo bis wo welcher Widerstand gemessen wurde und was das für die Widerstände der Leitungen zwischen den Steckdosen bedeutet.
geg: \(R_{1}=0,9\ \Omega\), \(R_{2}=0,65\ \Omega\), \(R_I=0,15\ \Omega\), \(A=1,5\ mm^2\), \(\rho=0,0178\ \frac{\Omega\cdot mm^2}{m}\)
ges: \(l_{X1}\), \(l_{X2}\)
Lös:
Der Widerstand einer Leitung steigt mit seiner Länge. Entsprechend setzen wir den geringeren der beiden an Steckdosen gemessenen Widerstände als den Widerstand für Steckdose X1 -> \(R_{2}=0,65\ \Omega\).
Der Widerstand der Leitung bis zu diesem Punkt ist abzüglich des Innenwiderstandes bis zur Stromkreisverteilung, somit ist der Widerstand für die NYM-Leitung 1:
\(R_{X1}=R_2-R_I=0,65\ \Omega-0,15\ \Omega=0,5\ \Omega\)
Im gemessenen Widerstand \(R_1\) ist der Widerstand \(R_2\) enthalten, da die Steckdosen in Reihe liegen. Somit ist der Widerstand der NYM-Leitung 2:
\(R_{X2}=R_1-R_2=0,9\ \Omega-0,65\ \Omega=0,25\ \Omega\)
Um nun die Leitungslängen zu ermitteln nutzen wir als Grundformel
\(R_{Ltg}=\frac{\rho\cdot l}{A}\)
und stellen diese auf die Länge \(l\) um
\(l=\frac{R_{Ltg}\cdot A}{\rho}\)
\(\Rightarrow l_{X1}=\frac{0,5\ \Omega\cdot 1,5\ mm^2}{0,0178\ \frac{\Omega\cdot mm^2}{m}}=42,13\ m\)
\(\Rightarrow l_{X2}=\frac{0,25\ \Omega\cdot 1,5\ mm^2}{0,0178\ \frac{\Omega\cdot mm^2}{m}}=21,07\ m\)
Berücksichtigen wir, daß es in jeder Leitung einen Hin- und Rückleiter gibt, so müssen die jeweiligen Längen noch halbiert werden.
Antw: Die NYM-Leitung 1 hat eine Länge von \(21,07\ m\) und die NYM-Leitung 2 eine Länge von \(10,54\ m\).
Aufgabe L
Eine \(40\ m\) lange Leitung NYM-J \(3x1,5\ mm^2\) ist von einer Stromkreisverteilung mit Zählerplatz zu einer Schutzkontaktsteckdose X1 im System 3/N/PE AC 50Hz 230V / 400V unter Putz verlegt. Der Innenwiderstand der Anlage an der Stelle der Stromkreisverteilung beträgt \(0,4\ \Omega\).

Berechne folgende Größen:
1) Innenwiderstand der gesamten Anlage bis zur Steckdose X1
2) Strom der fließt, wenn an der Steckdose ein Kurzschluss auftritt.
3) Spannungsfall über der NYM-Leitung bei einer Strombelastung von \(16\ A\).
geg: \(R_i=0,4\ \Omega\), \(\rho=0,0178\ \frac{\Omega\cdot mm^2}{m}\), \(l=40\ m\), \(A=1,5\ mm^2\), \(U=230\ V\), \(I=16\ A\)
ges: \(R_{i, ges}\), \(I_K\), \(\Delta U\)
Lös:
\(R_{Ltg}=\frac{\rho\cdot l}{A}=\frac{0,0178\ \frac{\Omega\cdot mm^2}{m} \cdot2\cdot40\ m}{1,5\ mm^2}=0,949\ \Omega=949\ m\Omega\)
\(R_{i, ges}=R_i+R_{Ltg}=0,949\ \Omega+0,4\ \Omega=1,35\ \Omega\)
\(U=R_{i, ges}\cdot I_K\Leftrightarrow I_K=\frac{U}{R_{i, ges}}=\frac{230\ V}{1,35\ \Omega}=170,37\ A\)
\(\Delta U=R_{Ltg}\cdot I=0,95\ \Omega\cdot 16\ A=15,2\ V\)
Antw:
Der Innenwiderstand der gesamten Anlage beträgt \(949\ m\Omega\). Der Kurzschlußstrom beträgt \(170,37\ A\). Der Spannungsfall über die Leitung von Strombelastung mit \(16\ A\) beträgt \(15,2\ V\).
Bewerte, den Spannungsfall aus Teilaufgabe 3.
geg: \(\Delta U=15,2\ V\)
ges: \(\Delta u\)
Lös:
\(\Delta u=\frac{\Delta U\cdot 100\%}{U}=\frac{15,02\ V\cdot 100\%}{230\ V}=6,53\%\)
Antw: Der Spannungsfall ist höher als \(3\%\) und somit zu hoch. Der Querschnitt muß auf \(4\ mm^2\) erhöht werden.